This article describes the mathematics behind a series of spiral-like prints and paintings. The math is simple, and not significant. It is, as far as I know, original. The article describes the generalization of three properties of the golden rectangle and a process for generating two sequences of rectangles, ratios, and number sequences that share mathematical properties with the golden rectangle, the golden ratio, and the Fibonacci numbers. The prints and digital drawings of progressive spiral-like images are generated from an Adobe Flash program developed for the project.
Abstract
Features of the golden rectangle, the golden ratio, and the Fibonacci numbers can be extended to other rectangles by generalizing the golden ratio formula and the Fibonacci number sequence. In this article I will describe a process for generating sequences of rectangles, ratios, and number sequences that share mathematical properties with the golden rectangle, the golden ratio, and the Fibonacci numbers. You can think of one sequence of rectangles, which is based on the silver means, as getting progressively taller and another shorter compared to a golden rectangle, the first rectangle in each sequence. These sequences of rectangles exhibit generalized properties of the golden rectangle. I list three properties which I extend. The formula for the golden ratio is a special case of general formulas for these sequences. You can create smaller rectangles with the same proportions by removing multiples or unit fractions of squares, and generate spiral-like curves in the process. The rectangles' ratios of long side to short side are the limits of the ratios of successive terms in numerical sequences which are generalized Fibonacci sequences.
 |
 |
 |
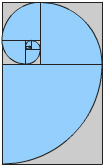
| Golden Rectangle |
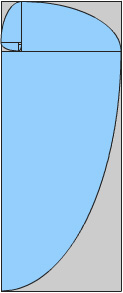
First Sequence |
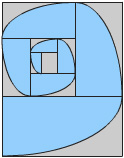
Second Sequence |
Contents
The Golden Rectangle
First Sequence of Rectangles
Second Sequence of Rectangles
Other Sequences
Summary
A Review of the Literature
Tables
References
The Golden Rectangle
The golden rectangle, a rectangle whose side lengths are in the golden ratio, has a number of interesting properties that have been studied since Euclid defined the extreme and mean ratio. [3][4][18][19]. Disregarding the usually exaggerated relationship of the golden rectangle to aesthetics and nature, I'll describe its construction then list three of its mathematical properties — ratio formula, spiral and number sequence:
| Construction. The golden rectangle can be constructed starting with a square, and using a diagonal across half the square as a radius to draw an arc that completes the rectangle. [15][19] |
| |
a. Construct a unit square.
b. Draw a line from the midpoint of one side to an opposite corner.
c. Use that line as the radius to draw an arc that defines the long dimension of the rectangle.
|
| |
 |
Ratio Formula. The golden rectangle's ratio of long side, a, to short side, b, can be described in a special formula: (a+b)/a = a/b. The fact that the ratio of a to b is equal to the sum of a and b divided by b is unique to the golden rectangle. This equation has a positive solution, the golden ratio, which is the irrational number (1+√5)/2, or approximately 1.61803398… [13][18]
Spiral. A golden rectangle can be used to construct new, progressively smaller rectangles with the same proportions as the first. When a square of the smaller side is removed from the rectangle, a new golden rectangle is the result. Square removal can be repeated, while drawing quarter-circles through each removed square leads to an approximation of a golden spiral. (See Wikipedia, Golden rectangle for a good diagram of the square removal, and Wikipedia, Golden spiral for more on spirals and why this spiral is only an approximation of a golden spiral. [19][20] Also, see Weisstein, Golden Rectangle for a diagram showing that a golden spiral passes through the corners of squares inscribed in a golden rectangle, but is not tangent to the rectangle's sides. [15]) The following image is of a golden rectangle with quarter-circles inscribed in successively smaller squares.

Inscribing quarter-circles in squares of a golden rectangle is just one of many ways to piece together a spiral-like curve from rectangles. Markowsky pointed out that you can generate spiral-like curves from any rectangle, other than a square. (See Markowsky, page 2. [10]) In his example he repeatedly divided larger rectangles in half. You can click on the image above for a demonstration of spiral-like curves generated from arbitrarily dimensioned rectangles. None of these methods for creating smaller rectangles and inscribing curves to simulate a spiral will create a true spiral because true spirals require that points along the spiral move away from a fixed center at a specific rate. (See Wikipedia, Spiral. [21]) The formula for a true golden spiral is sufficiently difficult that most articles about the golden rectangle, including this one, skip the formula in favor of the approximation.
Number Sequence. The golden rectangle's ratio of long side to short side, the golden ratio, is closely related to the Fibonacci numbers. The first few Fibonacci numbers (sequence A000045 in the On-Line Encyclopedia of Integer Sequences, OEIS, or Sloane's) are: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. [11] After 0 and 1, each term in the sequence is the sum of the two preceding numbers. As ever higher successive terms of the Fibonacci numbers are selected, the ratio of one number to the previous number gets closer to the golden ratio, approximately 1.61803398… [17] Knott shows why the Fibonacci ratios approach the golden ratio in his section, "The Ratio of neighbouring Fibonacci Numbers tends to Phi" [7]. Click here for a graphic of consecutive Fibonacci ratios approaching the golden ratio.
These three properties of the golden rectangle — three of the most interesting mathematical features — are shared by two sequences of rectangles that I describe below. You can think of the golden rectangle as the beginning of these two sequences. Imagine each rectangle in both sequences having a short side equal to the short side of a golden rectangle. In the first sequence, each rectangle becomes progressively taller. Each rectangle in the second sequence becomes progressively smaller, approaching a square. The formulas for the ratios of long side to short side and for the number sequences associated with the rectangles are general formulas with the golden rectangle being a special case.
First Sequence of Rectangles
I based the first sequence of rectangles on the silver means. Each ratio in this sequence is derived from a general formula for the values of the silver means:
where n are the consecutive integers, 1, 2, 3... [7][14]
Construction, First Sequence. I construct rectangles in the first sequence by starting with a unit square. After the golden rectangle, instead of using a diagonal across half the square to draw an arc that completes the rectangle, I draw a diagonal across a full square for the first rectangle. I add half a square and use a diagonal across the one and a half squares for the arc of the second rectangle. I add another half-square and use a diagonal across the two squares for the arc of the third. Following this process should create an infinite number of rectangles which are progressively taller.
| Example — Construction of the second rectangle in the sequence, after the golden rectangle: |
| |
a. Construct a unit square.
b. Add one half of a unit square on top of the first.
c. Draw a line from one corner to the opposite corner of the one and one half unit squares.
d. Use that line as the radius to draw an arc that completes the long dimension of the rectangle.
|
| |
 |
A similar process of construction can be repeated for each successive rectangle by adding an additional half-square. There is a formula that corresponds to this process of defining the long side. Since the construction process uses a unit square for the short side, a formula for the long side also describes the rectangle's proportions, and provides the solutions in Table 1.
| With the short side, b, as a unit square, the long side, a, is the number of half unit squares, n, used to construct the rectangle plus the length of the diagonal used to complete the long dimension: |
 |
| Simplified, this formula becomes the same as the general formula for the silver means that this sequence of rectangles is based on: |
 |
Therefore, the number of half unit squares, n, used to construct the rectangle determines the proportions and the solution. For n half unit squares = 1, this equation has the solution (1+√5)/2, the golden ratio. For n = 2, 3, and so on, the solution matches the desired values in Table 1. Since the long side length is based on the number of half-unit squares used to construct the rectangle, then for every n half-unit squares we can construct the nth rectangle in the sequence.
Note: In this sequence, to simplify equations I use m in formulas that call for a sequence of variables starting at 0. In other formulas I use n when the starting variable is 1 to avoid complicating formulas with m+1. For the same rectangle, n corresponds to m, and n equals m+1.
These rectangles have the following properties — ratio formulas, spirals, number sequences — in common with the golden rectangle.
Ratio Formulas, First Sequence. I can describe the rectangles' ratios of long side, a, to short side, b, in formulas which are generalizations of the formula for the golden ratio. The golden ratio formula is a special case of the same sequence of formulas. Whereas the formula for the golden ratio is (a+b)/a = a/b, the general ratio formula for this sequence of rectangles is:
(a + b)/(a – mb) = a/b
where
m is an integer designating the rectangle in the sequence. For the golden ratio,
m is zero. The formula for the first in this sequence of rectangles, after the golden rectangle, is: (
a+
b)/(
a–
b) =
a/
b. The second is: (
a+
b)/(
a–2
b) =
a/
b. For each successive formula in the sequence increase
m by one. See
Table 1.
These ratio formulas have a positive solution. The first is: 1 + √2, or approximately 2.41421356… See Table 1 for the first eight solutions in the sequence.
It will be helpful to convert the general ratio formula above to an equation in terms of m, to show that for every m in the ratio formula there is a corresponding solution matching the construction and the solutions in Table 1.
| I'll use a variation of a method from Wikipedia for calculating the golden ratio. [18] First I set the equation to a ratio, X. |
| |
(a + b)/(a – mb) = |
a/b = X |
| The right equation shows that a = bX, so I can substitute bX for a in the left equation. |
| |
(bX + b)/(bX – mb) = |
bX/b |
| Now I rearrange terms and simplify. |
| |
b²X + b² = |
b²X² – mb²X |
| |
X + 1 = |
X² – mX |
| |
X² – (m + 1)X– 1 = |
0 |
| Expressing this as a quadratic formula gives the solution for X: |
 |
Therefore, for every m designating a rectangle in the ratio formula there is a corresponding positive solution. For m = 0, this equation has a positive solution of (1+√5)/2, the golden ratio. For m = 1, 2, and so on, the solutions match the desired values in Table 1.
The general ratio formula shares a one-to-one relationship with the construction method. The variable n in the construction formula corresponds to m in the ratio formula. Since both formulas are equivalent to a/b (or long side, a, over short side, b), then every construction from n unit squares corresponds to a ratio formula, and they both share the same positive solution.
Spirals, First Sequence. I can use the rectangles to construct new, progressively smaller rectangles with the same proportions as the first. When multiples of squares of the smaller side are removed from the rectangle, a new rectangle with the same proportions is the result. Multiple square removals can be repeated. The unit squares to remove for each new rectangle increase from one for the golden rectangle, to two, three, and on for each rectangle in the sequence. Removing squares to generate a smaller rectangle with the same proportion is the most interesting aspect of this property. The fact that you can inscribe curves in each removed rectangle to approximate a spiral is secondary. [20] However, since much of the literature on the golden rectangle shows the spiral-like curve this process can create I'll show how this applies to the sequence of rectangles, as well.
After the golden rectangle, the rectangles in this sequence do not generate an approximation of a golden spiral. Spiral-like curves from these rectangles are made by joining opposite corners of removed multiples of squares with a quarter-ellipse or a curve that appears tangent to the inscribed rectangle. Neither these nor the spiral from a golden rectangle are true spirals. [21] Click on the image to view the sequence progression. For ease of construction the curve inscribed within each of these examples is a quadratic Bézier curve (created with Adobe Flash® ActionScript™), though you could use a quarter-ellipse as well.

Why does the removal process in fact produce smaller rectangles with the same proportions? There is a formula for the process of removing n unit square lengths from the long side to create a new short side, making the previous short side the new long side. This formula is the ratio of the smaller rectangle's sides in terms of the larger rectangle's sides: b/(a – nb). (Note, n is the number of unit squares to remove.)
| For every n unit squares to remove (see Table 1) the smaller rectangle proportions should match the larger. From the ratio formula above, the formula for the larger rectangle is: |
| |
(a + b)/(a – mb) = |
a/b |
| I can rearrange this formula: |
| |
ab + b² = |
a² – mba |
| |
b² = |
a² – mba – ab |
| |
b² = |
a(a – mb – b) |
| |
b/(a – (m+1)b) = |
a/b |
| Since m+1 equals n, the left side is the same as the ratio of the smaller rectangle in terms of the larger rectangle's sides, or b/(a – nb). Therefore, the smaller rectangle proportions are the same as the larger. |
| |
b/(a – nb) = |
a/b |
n in the construction formula corresponds to n in this formula for removing unit squares. Since both formulas are equivalent to a/b (or long side, a, over short side, b), every construction from n unit squares corresponds to a process of removing n unit squares to generate spiraling rectangles.
Number Sequences, First Sequence. The rectangles' ratios of long side to short side are approached by the ratios of successive terms in numerical sequences similar to the Fibonacci sequence. Click here for a graphic of consecutive number sequence ratios approaching the solution. In the Fibonacci number sequence, after two starting values, each number is the sum of the two preceding numbers. The Fibonacci number sequence is a special case of the sequences associated with the new rectangles. The number sequences associated with the new rectangles are generated with an additional coefficient for one of the terms. In the Fibonacci sequence that coefficient is one. The Fibonacci sequence can be written, where n is 1, as:
F(i) = nF(i–1) + F(i–2)
The numerical sequences for the new rectangles can be generated by n=2, n=3, and so on. Each number in the sequence associated with the first new rectangle, after two starting values, is generated by multiplying the previous number by 2, then adding the number before that [Sloane A000129]. The first numbers after two starting values of 0 and 1 are: 2, 5, 12, 29, 70… Each number in the sequence divided by the previous number approaches the rectangle's ratio of long to short side, approximately 2.414… Each successive sequence for each rectangle is modified by increasing the coefficient, n, by one.
I'll use a variation of Knott's method (see The Ratio of neighbouring Fibonacci Numbers tends to Phi) for relating number sequences to ratios to show proof that the ratios of successive pairs of numbers in the sequences (see Table 1) approach the ratio formula solutions as each sequence progresses. [7]
| The relationship of each sequence is: |
| |
F(i) = |
nF(i–1) + F(i–2) |
For three successive numbers in the sequence, especially large numbers, the ratios are to approach the same value. Therefore, F(i)/F(i–1) will be close to F(i–1)/F(i–2). Assume they are the same ratio, X.
| A: |
X = F(i–1) / F(i–2) = |
F(i) / F(i–1) |
| Using the relationship replace F(i) by nF(i–1)+F(i–2), and then simplify. |
| |
F(i) / F(i–1) = |
(nF(i–1) + F(i–2)) / F(i–1) |
| |
= |
nF(i–1) / F(i–1) + F(i–2) / F(i–1) |
| B: |
= |
n + F(i–2) / F(i–1) |
| Replace F(i)/F(i–1) in A by B. |
| |
X = F(i–1) / F(i–2) = |
n + F(i–2) / F(i–1) |
| F(i–2) / F(i–1) is the reciprocal of X, so: |
| |
X = |
n + 1/X |
| |
X² – nX– 1 = |
0 |
| Since m+1 is equivalent to n, this is the same as the ratio formula: |
| |
X² – (m + 1)X– 1 = |
0 |
Therefore, the ratios of successive terms in the number sequence approach the rectangle solutions. For n = 1, this quadratic equation, X²–nX–1 = 0, has the positive solution, X = (1+√5)/2, the golden ratio. For n = 2, 3, and so on, X matches the desired solution in Table 1. Since n in the construction formula corresponds to n in the quadratic equation above, every construction from n unit squares corresponds to a sequence. (Click here again for the graphic of consecutive number sequence ratios approaching the solution.)
| Continued Fractions. The first sequence of rectangles has associated continued fractions with patterns similar to the golden ratio: [1; 1,1,1…]. [14] After the golden ratio, the continued fractions for ratios in the sequence are: |
| |
[2; 2,2,2, …]
[3; 3,3,3, …]
[4; 4,4,4, …]
|
Second Sequence of Rectangles
Construction, Second Sequence. I construct the second sequence of rectangles, like the golden rectangle, by starting with a unit square. Instead of using a diagonal across half the square to draw an arc that completes the rectangle, I draw a diagonal across a quarter square for the next rectangle, across an eighth for the next, and a sixteenth for the next. Following this process creates an infinite number of rectangles which, sharing a short side with the golden rectangle, are progressively smaller, but always larger than a square of the short side. (See Table 2.)
| Example — Construction of the second rectangle in the second sequence, after the golden rectangle: |
| |
a. Construct a unit square.
b. Draw a line across the bottom eighth of the square.
c. Draw a line from one corner to the opposite corner of the eighth square.
d. Use that line as the radius to draw an arc that completes the long dimension of the rectangle.
|
| |
 |
A similar process of construction can be repeated for each successive rectangle by dividing the previous fraction of a square by 2 to start with a diagonal across a thirty-second, sixty-fourth, and so forth. There is a formula that corresponds to this process for defining the long side. Since the construction process uses a unit square for the short side, a formula for the the long side also describes the rectangle's proportions, and provides the solutions in Table 2.
| With the short side, b, as a unit square, the long side, a, is the sum of the fraction of a unit square used to construct the rectangle plus the length of the diagonal used to complete the long dimension: |
 |
| Simplified, this formula becomes: |
 |
Therefore, the fraction of a unit square, 1/n, used to construct the rectangle determines the proportions and the solution. For a fraction of a unit square = 1/2 or n = 2, this equation has a solution (1+√5)/2, the golden ratio. For fractions of a unit square = 1/4, 1/8, 1/16, (n = 4, 8, 16), and so on, the solution matches the desired values in Table 2. Since the long side length is based on the fraction of a unit square used to construct the rectangle, which is 1/n where n is a power of 2, then for every nth power of 2 we can construct the nth rectangle in the sequence.
Note: In this sequence, I use n to signify the starting variable is the first power of 2. I use m for variables starting at the zeroth power of 2. For the same rectangle, n corresponds to m, and n equals 2m.
These rectangles have the following properties — ratio formulas, spirals, number sequences — in common with the golden rectangle.
Ratio Formula, Second Sequence. I can describe the rectangles' ratios of long side, a, to short side, b, in formulas which are generalizations of the formula for the golden ratio. The golden ratio is a special case of the same sequence of formulas. Whereas the formula for the golden rectangle is (a+b)/a = a/b, the general ratio formula for the second sequence of rectangles is:
b/(a – b/m) = a/b
where m is a power of 2. This new formula applies to the golden rectangle when m is the zeroth power of 2, or 1.
Here is an alternative version of the same formula:
(a + mb)/ma = a/b
| Since I have just claimed that when m = 1 the new formula applies to the golden rectangle, it should be equivalent to (a+b)/a. This shows that (a+b)/a = b/(a–b). (See Wikipedia, Golden ratio, Short proofs of irrationality [18]): |
| a/b = |
(a + b)/a |
| a2 = |
ab + b2 |
| a2 – ab = |
b2 |
| a(a – b) = |
b2 |
| a/b = |
b/(a – b) |
The formula for the first in this sequence of rectangles, after the golden rectangle, is: b/(a – b/2) = a/b. The second is: b/(a – b/4). For each successive rectangle in the sequence increase m to the next power of 2.
These ratio formulas have unique positive solutions. The first is: (1+ √17)/4, or approximately 1.281… See Table 2 for the first eight solutions in the sequence.
I'll convert the general ratio formula above to an equation in terms of m, to show that for every m in the ratio formula there is a corresponding solution matching the construction and the solutions in Table 2, as I did for the first sequence of rectangles.
| First I set the equation to a ratio, X. |
| |
b/(a – b/m) = |
a/b = X |
| The right equation shows that a = bX, so I can substitute bX for a in the left equation. |
| |
b/(bX – b/m) = |
bX/b |
| Now I rearrange terms and simplify in three steps. |
| |
b² = |
b²X² – b²X/m |
| |
1 = |
X² – X/m |
| C: |
X² – X/m – 1 = |
0 |
| Expressing this as a quadratic formula gives the solution for X: |
 |
Therefore, for every m designating a rectangle in the ratio formula there is a corresponding positive solution. For m = the zeroth power of 2, or 1, this equation has the positive solution of (1+√5)/2, the golden ratio. For m = 2, 4, 8, 16, and so on, the solutions match the desired values in Table 2.
The general ratio formula shares a one-to-one relationship with the construction method. The variable n in the construction formula corresponds to a power of 2 represented by m in a ratio formula. Since both formulas are equivalent to a/b (or long side, a, over short side, b), then every construction from n unit squares corresponds to a ratio formula, and they both share the same positive solution.
Spirals, Second Sequence. I can use the rectangles to construct new, progressively smaller rectangles with the same proportions as the first. When unit fractions of squares of the smaller side are subtracted from the rectangle, a new rectangle with the same proportions is the result. The fraction of a square removal can be repeated. The fraction of a unit square to subtract for each new rectangle decreases from one for the golden rectangle, to a half, a fourth, an eighth, and on for each rectangle in the sequence. As I said in the first sequence, removing squares to generate a smaller rectangle with the same proportion is the main point.
Like the first sequence of rectangles, those in this sequence do not generate an approximation of a golden spiral. Spiral-like curves from these rectangles are made by joining opposite corners of removed fractions of squares with a quarter-ellipse or a curve that appears tangent to the inscribed rectangle. Neither these nor the spiral from a golden rectangle are true spirals because true spirals require that points along the spiral move away from a fixed center at a constant rate. (See Wikipedia, Spiral. [21]) Click on the image to view the sequence progression.

Why does the removal process in fact produce smaller rectangles with the same proportions? There is a formula for the process of removing fractions of square lengths from the long side to create a new short side, making the previous short side the new long side. This formula is the ratio of the smaller rectangle's sides in terms of the larger rectangle's sides: b/(a–b/m). (Note, b/m is the fraction of a unit square to remove.)
| For every b/m unit squares to remove (see Table 2) the smaller rectangle proportions should match the larger. From the ratio formula above, the formula for the larger rectangle is: |
| b/(a – b/m) = a/b |
The left side is the same as the ratio of the smaller rectangle in terms of the larger rectangle's sides. Therefore, the smaller rectangle proportions are the same as the larger. |
n in the construction formula corresponds to a power of 2 represented by m in this formula for removing unit squares. Since both formulas are equivalent to a/b (or long side, a, over short side, b), every construction from 1/n fractions of a square corresponds to a process of removing b/m unit squares to generate spiraling rectangles.
Number Sequences, Second Sequence. The rectangles' ratios of long side to short side are approached by the ratios of successive terms in numerical sequences similar to the Fibonacci sequence. Click here for a graphic of consecutive number sequence ratios approaching the solution. In the Fibonacci number sequence, after two starting values, each number is the sum of the two preceding numbers. The Fibonacci number sequence is a special case of the sequences associated with the new rectangles. The number sequences associated with the new rectangles are generated by dividing one term by a power of 2:
F(i) = F(i–1)/m + F(i–2)
where m is a power of 2. This applies to the golden rectangle and Fibonacci sequence when m is the zeroth power of 2, or 1. After the golden rectangle the numerical sequences for new rectangles can be generated by m=2, 4, 8, and so on, with m increasing each time to the next power of 2. The sequences produced are not integer sequences.
Each number in the sequence associated with the first rectangle after the golden rectangle, is generated by dividing the previous number by 2, then adding the number before that. The first numbers are: 0, 0.5, 0.25, 0.625, 0.5625. Each number in the sequence divided by the previous number approaches the rectangle's ratio of long to short side, approximately 1.281…
In these numerical sequences, the ratios of number pairs approach their rectangle's ratio gradually more slowly than does the Fibonacci sequence. It is necessary to select number pairs ever higher before it becomes apparent that the ratio of pairs is approaching the associated rectangle's ratio.
I can use a version of the same proof from the first sequence of rectangles, applying Knott's method (The Ratio of neighbouring Fibonacci Numbers tends to Phi) to show that the ratios of successive pairs of numbers in the sequences (see Table 2) approach the ratio formula solutions as each sequence progresses. [7]
| I can replace n in the prior proof with 1/m, where m is a power of 2. Each sequence is: |
| |
F(i) = |
(1/m)F(i–1) + F(i–2) |
| For three successive numbers in the sequence, especially large numbers, the ratios are to approach the same value. Therefore, F(i+2)/F(i+1) will be close to F(i+1)/F(i). Assume they are the same ratio, X. |
| |
X = F(i–1) / F(i–2) = |
F(i) / F(i–1) |
| Using the relationship replace F(i) by (1/m)F(i–1) + F(i–2), and then simplify. Since this is a version of the same proof from the first sequence of rectangles, except n is now 1/m, I'll skip to the last line. |
| |
X² – (1/m)X – 1 = |
0 |
Therefore, the ratios of successive terms in the number sequence approach the rectangle solutions. For m = the zeroth power of 2, this quadratic equation has the positive solution, X = (1+√5)/2, the golden ratio. For each m = 2, 4, 8, and so on, X matches the corresponding solution in Table 2. Since n in the construction formula corresponds to a power of 2 represented by m in a quadratic equation above, every construction from n unit squares corresponds to a sequence. (Click here again for the graphic of consecutive number sequence ratios approaching the solution.)
| Continued Fractions. The second sequence of rectangles has periodic continued fractions. After the golden ratio, the continued fractions for ratios in the sequence are: |
| |
[1; 3,1,1,3,1,1,3,1,1, …]
[1; 7,1,1,7,1,1,7,1,1, …]
[1; 15,1,1,15,1,1,15,1,1, …]
[1; 31,1,1,31,1,1,31,1,1, …]
[1; 63,1,1,63,1,1,63,1,1, …]
[1; 127,1,1,127,1,1,127,1,1, …]
[1; 255,1,1,255,1,1,255,1,1, …] |
Other Sequences
The process I describe above might be used for finding more sequences of rectangles with the same properties. In Table 3. Third Sequence of Rectangles, I show another sequence of ratios and number sequences that can be used to develop rectangles and spirals. This sequence continues the theme started above. It differs from the first and second sequences above, however, in that the first ratio in the sequence is not the golden ratio. It is the silver ratio. [14]
| Continued Fractions. The third sequence of rectangles has periodic continued fractions. The continued fractions for ratios in the sequence are: |
| |
[2; 2,2,2,2,2,2,2,2,2, …]
[1; 4,1,1,4,1,1,4,1,1, …]
[1; 6,1,1,6,1,1,6,1,1, …]
[1; 8,1,1,8,1,1,8,1,1, …]
[1; 10,1,1,10,1,1,10,1,1, …]
[1; 12,1,1,12,1,1,12,1,1, …]
[1; 14,1,1,14,1,1,14,1,1, …] |
Summary
This completes the description of a process for generating sequences of rectangles, ratios, and number sequences that share properties with the golden rectangle. Each sequence of rectangles has a method of construction based on multiples or fractions of a unit square and three properties: a formula for the ratio of long to short side that is a generalized version of the golden ratio formula; a method for removing squares or fractions of a square to construct new rectangles with the same proportions and to generate spiral-like curves; and, a ratio of long side to short side that is the limit of the ratios of successive terms in a numerical sequence based on a generalization of the Fibonacci number sequence.
I have given examples of only the first few rectangles in each sequence, but I believe that the possible rectangles might continue infinitely, with the golden rectangle being the first rectangle in each sequence. I think it's reasonable to conclude that some of the golden rectangle's most interesting mathematical properties are not unique.
A Review of the Literature
Researching the literature, you'll find several writers who debunk the false claims around the aesthetics of the golden rectangle while listing its special mathematical features. I hope that showing these features can be extended to other rectangles supports the position that the aesthetics of the golden rectangle are exaggerated.
The math in this article is not original given that the properties of the golden rectangle are well established. I borrow proofs that are readily available from Wikipedia (see Golden ratio, Short proofs of irrationality), and from Dr. Ron Knott (see The Ratio of neighbouring Fibonacci Numbers tends to Phi). [7][18] Given the huge interest in this topic, I have expected to find that someone else already extended properties of the golden rectangle to other sequences of rectangles. However, as yet I have found no more than a suggestion of the potential for the properties of the golden rectangle to be extended.
The fact that you can generate spirals from any rectangle, other than a square, is not new. (See Markowsky, page 2. [10]) One of the sequences I describe is based on the silver means which has been well documented by Knott. (See Solving Quadratics with Continued Fractions, The Silver Means). [7][14] It's been eighty years since Jay Hambidge described a design system incorporating the golden ratio and root rectangles based on √2, √3, √4, and √5. [5] Markowsky's point about spirals, Knott's suggestion of a rectangle sequence in the silver means, and Hambidge's rectangles each imply that you can extend properties of the golden rectangle. Yet the most commonly documented mathematical properties of the golden rectangle have seldom been recognized in other rectangles. In this article I generalize three properties of the golden rectangle to two sequences. I suggest this process may be used for finding more sequences of rectangles with the same properties.
Books and articles extolling the wonders of the golden ratio usually show how the golden rectangle can be used to approximate a golden spiral, how it relates to the golden ratio, and to the Fibonacci numbers. The implication is that art and architecture employing the golden rectangle is superior by association. Thankfully, the mathematicians George Markowsky of the University of Maine and Keith Devlin of Stanford University, as well as astrophysicist Mario Livio, argue against the excessive claims made for the appearance of the golden ratio in art, architecture, and the antiquities.
These writers separate fact from fiction regarding the aesthetics of the golden rectangle. They also demystify the occurrence of the golden ratio in nature. Keith Devlin has published at least two articles that bust the myths, available at MAA Online. The first was in 2004: Good stories, pity they're not true. The second in 2007: The Myth That Will Not Go Away. [1][2] George Markowsky countered many of the myths in his 1992 article, Misconceptions About The Golden Ratio. Markowsky was particularly thorough addressing the myths about design of the Great Pyramid of Cheops, the design of the Parthenon, and the paintings of Leonardo da Vinci. [10]
The following sources include comprehensive general information, and the writers and contributors either debunk false claims for the golden rectangle's aesthetics, or qualify them with reference to the fact that others do not necessarily believe the claims:
- Golden Ratio, Wikipedia. The contributors generally question the practice of applying the golden rectangle to aesthetics. [18]
- Golden Rectangle, Wolfram MathWorld. The author, Eric Weisstein, concentrates on math, and mostly avoids aesthetics. [15]
- Fibonacci Numbers and the Golden Section, Ron Knott's web site. Knott qualifies his survey of the Art, Architecture and Music by pointing out that the use of the golden section in the arts is a matter of opinion and speculation. [7]
- The golden ratio and aesthetics, by Mario Livio. Livio cites psychology experiments while addressing myths of the golden rectangle in the arts. [9]
- The Golden Ratio: The Story of PHI, the World's Most Astonishing Number, a book by Mario Livio. Livio addresses the art, architecture and other myths in depth. [8]
In the interest of providing a balance of references, I refer you to:
Design systems have been based on various sets of rectangles, some relating to the golden rectangle. The following describe several that use construction methods similar to those of the rectangles I describe:
- The Elements of Dynamic Symmetry, Jay Hambidge. Hambidge described a design system incorporating the golden ratio and root rectangles — rectangles with the proportions 1:√2, 1:√3, 1:√4, and 1:√5. The root rectangles are developed using a simple method where each rectangle is constructed from an arc of the diagonal of the previous rectangle. [5]
- Canons of page construction, Wikipedia. The contributors describe various systems for designing books, especially those by Jan Tschichold, which are developed from simple numerical ratios as well as the golden ratio. [16]
- ISO 216, Wikipedia. The International Organization for Standardization specifies sizes of writing paper based on the ratio, 1:√2.
- Timeless by Design, Valrie Jensen. Artist Valrie Jensen describes 12 rectangles, some of which are constructed in a way similar to the golden rectangle and Hambidge's root rectangles.
Copyright 2007 Joe Bartholomew

